统计学是数据分析的基础，很多人只会用平均数去分析这往往是粗糙的，不准确的。如果掌握了统计学，那么我们就能以更多更科学的维度去分析数据。本文将围绕统计学的几大特性进行简单介绍，希望对大家的工作有所帮助。

统计量的描述方式

集中性

1.平均数：Mean

是表示一组数据集中趋势的量数，是指在一组数据中所有数据之和再除以这组数据的个数。

2.众数：Mode

是一组数据中出现次数最多的数值，有时众数在一组数中有好几个。

3.中位数：Median

把所有数据按顺序进行排列，分布在最中间的值。

样本总数为奇数时，中位数为第(n 1)/2个位置对应的值；

样本总数为偶数时，中位数是第n/2个，第(n/2) 1个值的平均数。

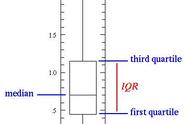
4.四分位数：Quartile

把所有数值由小到大排列并分成四等份，处于三个分割点位置的数值。

第一四分位数 (Q1)，指该样本中所有数值由小到大排列后第25%的数字；

第二四分位数 (Q2)，又称“中位数”，指该样本中所有数值由小到大排列后第50%的数字；

第三四分位数 (Q3)，指该样本中所有数值由小到大排列后第75%的数字。

四分位数

离散性

1.四分位距 ：Interquartile range

第三四分位数与第一四分位数的差距称四分位距，IQR=Q3-Q1。

四分位距

2.异常值：Outlier

小于Q1-1.5(IQR)或者大于Q3 1.5(IQR)的值，处理数据环节我们需要将异常值剔除。

3.极差：Range

一组数据中最大值与最小值之间的差值，R=Xmax-Xmin。

4.方差：Variance

每个样本值与全体样本值的平均数之差的平方值的平均数。

5.标准差：Standard Deviation

总体各单位标准值与其平均数离差平方的算术平均数的平方根。它反映组内个体间的离散程度。

分布形态

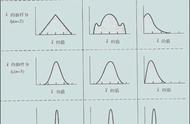
1.概率分布：Probability distribution

用于表述随机变量取值的概率规律。事件的概率表示了一次试验中某一个结果发生的可能性大小。若要全面了解试验，则必须知道试验的全部可能结果及各种可能结果发生的概率，即随机试验的概率分布。

2.置信区间：Confidence interval

指由样本统计量所构造的总体参数的估计区间，置信区间展现的是这个参数的真实值有一定概率落在测量结果的周围的程度，其给出的是被测量参数的测量值的可信程度，一般较为常用的是95%的置信区间。

3.正态分布：Normal distribution

随机变量X服从一个数学期望为μ，方差为σ²的正态分布，记为N(μ,σ²;)

随机取一个样本，有68.26%的概率位于距离均值μ有1个标准差σ内；

有95.45%的概率位于距离均值μ有2个标准差σ内；

有99.73%的概率位于距离均值μ有3个标准差σ内。

正态分布概率分布图