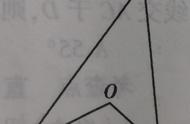
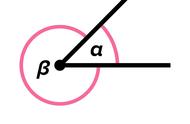
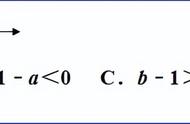拿到题目不要慌，条件问题找联系，拿上条件找全等，整完全等用性质，中点和高平分线，不要忘了中垂线。

初中数学相对于高中知识来讲真的是非常基础非常简单的一个阶段。但是总有很多学生在不同的阶段掉队。全等三角形的学习，相对于几何学习的一个根基，是初中学生最容易掉队的一个阶段。

很多学生可以说学完了整个初二阶段，还不明白学习全等的意义，拿上题目不会做，只会乱往里面套条件，样式看起来和标准答案差不多，内在确实乱七八糟稀里糊涂。

全等三角形可以说是平面几何和立体几何最重要的知识基础。全等三角形学好了，学精了，可以说整个初高中阶段的几何都不会出问题。

如果说这个阶段的问题没有解决，那么以后无论学到哪个阶段，知识学的再好，也总会因为这个基础无法取得高分。

我本文给出的第一段的顺口溜就是核心。几何问题，拿本章为例，书本上的概念，判定方法，以及等腰三角形，直角三角形，角平分线，中垂线，等边三角形等等这些性质，这是书本上最基础的东西，首先要多记多理解，不能只是背会，而是要有自己的理解。

其次拿上题目后，读题要慢一些，我提倡边读题边看图，将题目中的条件用不同的符号标注在图中，例如A B＝CD

,∠1＝∠2，这些条件，一定要用铅笔，标注在图中，因为这样就不用回过头来看条件，不会漏掉条件。

条件转化到图上之后要从条件中去看看是否存在需要证明的条件，首先得有一眼看出图中哪些三角形是全等的，这个能力通过多练题慢慢会提高。这样你才有做题的方向。

一般稍难一点的题目，我们需要证全等的三个条件题目中都会把需要的条件隐藏起来，需要用很多知识和方法去找需要的条件，类似的有，平行线证角相等，同角或等角的余角相等，等式的性质证角或边相等，公共边公共角等等方法。

除此之外还有很多难题，题目给的条件并不是我们需要证明的全等的条件，这类题目往往把能证全等的三角形证一遍，然后呢用全等的性质，把证出的全等三角形的边和角相等作为条件再去证明我们需要证明的三角形。

需要讲解的知识还有很多，要想将本章学好肯定不是一个文章就能解决的。

如果你家有孩子刚好上到现在又刚好有疑惑可以欢迎大家老和我探讨或者问我方法。

希望所有的孩子学习更上一层楼。如果您觉得本文还有帮助，记得分享和点赞，谢谢