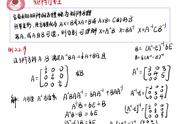一篇文章搞定矩阵

——第三篇 矩阵题型总结和解题方法

矩阵这一章节较为重要，因此题型也较多，下面先按照形式分成几大类，大类中按照知识点的不同再细分为小类。

一，代数运算型

标题看似简单，实则暗藏玄机。单纯的从题目的大致长相上这一类题都很相似（都给出了矩阵的数值），但实际上可以考察很多不同的知识点，欲知后事如何，且看下文：

（一），矩阵的乘法

（这一块不细讲，只是作为简单的分类）作为一个比较基本的运算，其往往是作为一个题目的部分而出现，比如作为利用逆矩阵运算的最后一步，如X=AB-1而且AB均已知。与行列式结合也是一个不错的选择，就像我要考你一个爪型行列式的运算，但是这个行列式，需要用矩阵的乘法算出来。总而言之，还是比较基础的。

（二），矩阵的秩和等价标准型

给出矩阵求矩阵的秩，或者求其等价标准型也是比较基础，主要是考察运算思路，这里稍微介绍一下等价标准型的求法：

首先将矩阵化为阶梯型后，利用行变换从下往上消，直至不能再消去，然后用列变换操作继续消去，最后调整顺序把剩下的数按主对角线排布即可。空口无凭，举例如下：

一看第三行只有一个8，毫不犹豫的直接把2和7抹去。看见两个1在一起，用第一行减去第二行，消去！而后采用列变换，用二三列的1消去前两行剩下所有的数字，最后-8可以直接看成1，调整顺序就得到左上角三个1其余全是0的矩阵。

（三），求逆矩阵

这里的求逆矩阵一般都是AX=B，然后AB已知求X之类的形式，主要有两种两种解法，先说笨的：那就是先求出A-1，然后用A-1乘以B得到X。显然并不容易，两步都很繁琐，如果我们非得在这笨拙的方法中找出一点技巧的话，那就是二阶矩阵的逆矩阵可以直接凭借公式写出，公式如下：

这里不做证明，因为重头戏在后面，第二种简单的方法就是把AB的矩阵写在一起，利用行变换把左侧化成E，右边得到的就是X。符号语言如下图；

我们举个例子具体说明一下：