(S△ABC)^2=

(a b c)(a b-c)(c a-b)(c-a b)/16

=[(a b c)/2][(b c-a)/2][(a c-b)/2][(a b-c)/2]

=p(p-a)(p-b)(p-c)

海伦公式：p=(a b c)/2

S△ABC=√[p(p-a)(p-b)(p-c)]

最后再举一个例子。

已知：

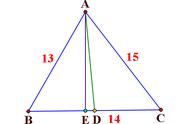
△ABC的三边长分别为4,13,15

求：S△ABC

解：p=(a b c)/2

=(4 13 15)/2=32/2=16

S△ABC

=√[16×(16-4)×(16-13)×(16-15)]

=√(16×12×3×1)=√576=24

S△ABC=24

方法二：如图所示作辅助线

解方程可得高为12

S△ABC=(4×12)/2=48/2=24

对比可以发现，如果只知道三角形的三边长，海伦公式可直接求出三角形面积，而避免了作辅助线、列方程等过程，运用起来非常简捷。