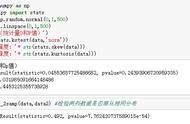
上节讲解了如何将外界的数据导入到SPSS中，本节将重点讲解如何在SPSS中计算数据的离散趋势和集中趋势以及如何判断一组数据是否符合正态分布。

集中趋势是指一组数据向某一中心靠拢的程度。常用于描述集中趋势的指标有均数、几何均数及中位数等。均数适用于正态分布和无极端值的对称分布的数据、几何均数适用于正偏态数据而中位数则是适用于偏态数据、截尾数据以及任何分布的数据。这三个指标中，中位数的适用范围最广，但是由于中位数的计算未使用全部的数据，易导致信息丢失，所以在能使用均数时应优先使用均数。

离散趋势用于描述数据偏离中心位置的趋势。常用于描述离散趋势的指标有标准差、方差、四分位数间距、极差和变异系数等。标准差是方差开平方后所得到的值，它的单位和观察值的单位是一致的，所以相较于方差标准差是更常使用的指标。标准差适用于正态分布、无极端值的对称分布。四分位数间距则适用于偏态分布。变异系数用于比较两组单位不同或单位相同但均数相差悬殊的数据的离散程度。

在数据的描述中，应当将集中趋势和离散趋势结合起来。医学论文中在描述一组数据时，通常正态分布的数据会选择均数±标准差，非正态分布会选择中位数（四分位数间距）的形式来进行描述。

由于均数、中位数、标准差和四分位数间距使用较多，因此本文仅示范用SPSS计算均数、中位数、标准差和四分位数间距。下面，以随机选择的两个班级15名同学的选择题得分为例来讲解SPSS中这些指标的计算。

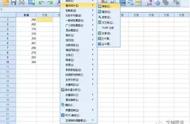
点击分析——描述统计——探索；将选择题得分选入因变量列表即可，最后点击确定。