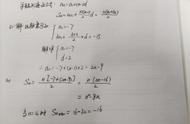按一定次序排列的一列数称为数列，而将数列{an} 的第n项用一个具体式子（含有参数n）表示出来，称作该数列的通项公式。这正如函数的解析式一样，通过代入具体的n值便可求知相应an项的值。而数列通项公式的求法，通常是由其递推公式经过若干变换得到。

　　求数列通项公式的方法非常多，常见的有观察法，累加法，累乘法，待定系数法，倒数法，解方程法，阶差法，和与通项的关系法等。除此之外，我们还会遇到一些难度较大的方法，比如，对数法，特征根法，不动点法，奇偶分析法等等。

1·观察法：

【评注】

由数列的前几项求通项公式的常用方法为观察法，即观察第n项与项数的关系，在观察时，往往需要对各项进行变形，变成形式类似，关系统一的形式，之后利用归纳得出通项公式。注意有限项归纳出的通项公式往往不唯一，有些通项公式可以利用分段函数来表示。

2·累加法：

【评注】

数列递推关系式中满足后项与前项的差等于常数，则为等差数列，直接利用等差数列的通项公式求解，如果满足后项与前项的差等于一个函数，则考虑利用累加法进行求解。

3·累乘法：