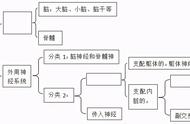
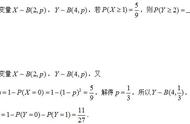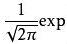左：高尔顿 右：凯特勒

那么这么厉害的正态分布到底讲的是什么呢？别急，我们先来看看高尔顿是怎么研究的。

1877 年，高尔顿设计了一个叫高尔顿钉板的实验，模拟正态分布的性质：

实验视频只需14秒！

高尔顿钉板试验内容：

有一块贴在墙上的木板，木板上有一些水平钉子，它们彼此的距离均相等。让一些小球从木板上方的入口处自由落体，经过一次次碰撞后，这些小球最终掉落到下方的竖槽中。

知道了实验内容后，我们来看看高尔顿钉板实验的细节：

弹珠往下滚的时候，撞到钉子就会随机选择往左边走，还是往右边走：

这些小球最终的分布位置如下图：

像这种左右对称，两头低，中间高的曲线我们称它为正态分布，又因其曲线呈钟形，人们又经常叫它钟形曲线。

为什么正态分布会如此常见呢？

咳咳，接下来就是今天内容的重点了（敲黑板）！

这个问题可以用中心定理（central limit theorem）来回答：在适当的条件下，大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布。

中心极限定理提出者——棣莫弗

这个定理可以这么理解：

生活中各种各样的因素就像高尔顿钉板实验中的钉子一样，对我们各个方面产生了大大小小的影响，使得最后的结果分布趋近于正态分布；

但中心定理并不是万能的，他拥有两个很重要的前提：

首先，第一个前提就是取样需要随机。

这个前提相信大家可以很好地理解，如果我们抽取的人的时候，只抽抽长的高的或者只抽取长得矮的人，那么结果自然不符合正态分布。

第二，影响结果的因素是相互独立或者是相互影响比较小的。

也就是说，如果影响结果的因素之间并没有太大的关系，那么这些因素可以看成是相互独立的，这样结果才能符合正态分布。

以身高为例，影响一个人长高的因素有很多，例如：

父母长得高还是矮

营养是否跟得上

是否热爱运动

......

等等

父母长得高还是矮对营养的补充没有很大的关系，跟是否热爱运动也没有关系，所以可以看成是相互独立的因素，所以身高的人群分布曲线自然就符合正态分布。

这时刻可能有人会问，如果这些因素不独立，甚至是有紧密的联系会怎么样呢？

我们来看看下面这个例子：人均财富分布（马太效应）。

从下图可以发现：富人的有钱程度（可以一直向x轴右端延伸）远远超出穷人的贫穷程度，即财富分布曲线有右侧的长尾。