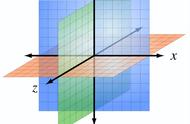
这样，维度由二维上升到三维，同时，我们得到一个棱柱体，为什么不是立方体呢？因为向量（1，4，6）和（4，-1，7）之间的夹角不是90度，如下图：

图形失真，向量（2，1，-1）和另两个向量其实是垂直的

讲到这里，我们基本清楚行列式是什么了，一行代表一个向量，一列代表一个空间维度，每个元素，对应一个空间坐标。

那么，行列式为什么要计算呢？回头看上面的二阶行列式，它的计算结果是-17，而对应向量所围合的矩形的面积是17，两者相等。这是巧合吗？

假设两者是有关联的，即二阶行列式的计算结果与对应向量围合的矩形面积相等，那三阶行列式的计算结果会不会与对应向量围合的棱柱体的体积相等？

那我们就来算一下吧。先计算行列式：

然后，再计算由向量（1，4，6）、（4，-1，7）和（2，1，-1）围合的棱柱体的体积。因为向量（2，1，-1）与另两个向量垂直，我们用它来做棱柱体的高，用向量（1，4，6）和（4，-1，7）围合的平行四边形做底面。

那么棱柱体的高为：

平行四边形的面积用三角函数面积公式S=1/2ab sinc来求，先用向量的内积除以向量长度的乘积，求其夹角的余弦：