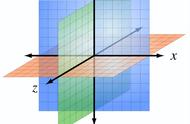
互换了Y和Z轴，但不影响结果

3、行列式的计算结果并不重要，更多的时候，我们只需要判断它为不为零。有一种行列式计算结果为零的情况，就是行列式的两行或两列元素完全相同。我们想像一下，如果两行元素完全相同，是不是相同于在当前的向量空间里，有两条线是完全重叠的。

这就好比纸箱压成了纸片，体积可不就是零嘛！

所以，当行列式的计算结果为零时，说明至少有一个维度里，是没有向量的。所以，我们用行列式来判定向量空间的饱满度。后面要学到的向量组的线性相关与线性无关，说白了就是向量空间饱满度的问题。

比如在我们生活的现实世界里，一个纸箱以它的长、宽、高为三组向量，相对于三维空间，纸箱的向量空间就是饱满的，我们没法再找到一个向量（或直线）与它的长、宽、高同时垂直，那么长、宽、高就是线性无关的。一张纸片以它的长、宽为两组向量，相对于三维空间，纸片的向量空间是不饱满的，我们可以用一条竖直向量（或直线）与它的长、宽同时垂直，那么长、宽就是线性相关的。这些都可以从行列式的计算结果里找到答案。