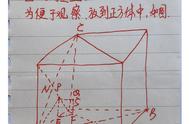
细胞自动机是一种非常简单的计算形式，它的起源很难确定，但早在20世纪50年代初，洛斯阿拉莫斯的数学家斯坦尼斯劳·乌兰姆就用第一台数字计算机来处理过随时间演化的图案。他称之为“递归定义的几何学”。

第一个真正的细胞自动机可能是由乌兰姆的密友，著名的数学家和计算机科学家约翰尼·冯·诺依曼发明的。乌兰姆建议冯·诺依曼尝试在人工宇宙中构建基于规则的机器，这有助于模拟自我复制。冯·诺依曼选择了一个棋盘宇宙，其中每个方块代表一个遵守一套规则的细胞。这就是第一个细胞自动机。

细胞自动机是一种非常简单的计算形式。当你观察周围的世界时，你所看到的事物是处于一定的位置和状态的。生物细胞位于其他细胞丛中的特定位置，其状态要么是活着的，要么是死亡的。你可以想出其他非生物学的例子，但正是这一生物学例子真正推动了细胞自动机的诞生。

假设我们有一个细胞，它有特定的位置和状态。那么，影响细胞状态的因素是什么？

在大多数情况下，你会假设细胞的状态受其周围细胞的影响。然而重点是在没有细胞的几英里外发生了什么。这是一种局部化假设，也是大多数经典物理学固有的假设。例如，波是由一个微分方程描述的，此微分方程将一个点上发生的事情与该点周围无穷小的区域中发生的事情联系起来。

你或许会认为局部假设过于严格，因为它不允许远程交互，但在物理世界中，远程交互是通过点对点移动的影响而产生的。远程交互是通过只依赖于局部相互作用的脉冲和波的传播产生的。

我们最终假设影响细胞自动机的因素是环境。假设细胞的状态仅受当地环境的影响。然而在大多数情况下，我们会将假设范围缩到更小，认为细胞的状态只受其当前状态和相邻细胞状态的影响。

根据此想法，假设最开始你有一个初始的细胞群，且每个细胞都有一个初始状态，然后你让这个细胞群进行分裂。此操作通常要在几段不同时间内完成——你也可以在连续时间内运行细胞自动机，但这样操作起来难度更大。

当时间为t时，你获得了所有细胞的位置和状态；然后运用规则，根据每个细胞的当前状态和相邻细胞的状态推测出此细胞的状态。当时间为t 1时，所有细胞都能按照相同的规则改变其状态。

要明确定义细胞自动机，必须确定细胞可能的状态、细胞的初始排列情况和更新规则。那么你希望这种计算可以用来做什么呢？

你可以将细胞自动机视为用于描述许多物理现象的经典微分方程的数字版本。 但是，细胞自动机并不像你认为的那样容易分析。典型的细胞自动机中使用的规则的性质使得我们很难预测在任意给定的初始条件下细胞将发生什么变化。

例如，你可能会问，给定的一组细胞是否会振荡、消失或无约束地生长，但很难得出问题的答案。细胞自动机之所以吸引人，是因为它们不可预测，而且大多无法测量。

细胞自动机是本地规则如何影响全局组织行为的例子，或者至少是看起来像全局组织行为的例子。

能够识别轮廓的细胞自动机

我们用一个矩形网状细胞群作为执行某些有用操作的细胞自动机示例，其中每个细胞都为黑色或白色并处于初始设置状态：

每个细胞在下一个步骤都将遵守如下规则：

如果一个细胞为黑色，与之相邻的细胞为白色，那么此细胞将保持黑色，反之，细胞将变为白色。

这里，相邻细胞指的是水平或垂直相邻的任何细胞。

你认为这个所有细胞都遵守的简单规则将导致怎样的结果？

你或许会感到惊讶，此规则仅将原始形状的轮廓保留为黑色：

换句话说，此规则成功地筛选出了形状的轮廓。请注意，任何细胞都只使用了本地信息，但却成功地提取了我们可能认为是全局的东西，即轮廓。

这种现象与在体育赛事中人群中的成员被要求在特定时间举起带有不同的图片和图案的卡片的情况相同。

应用本地规则可以产生全局模式。