2021年陕西中考在6月21日正式结束，数学考试是在6月19日下午进行的，在6月19日的下午，从网上就流传出部分的题目（部分信息与数据与真题略有偏差），虽然没有看到全卷，但对今年的中考数学的难度有了一个预判，试卷结构和题型发生了变化，重难点考点没变，但题目的难度明显降低了，试卷更注重对学生基本数学素养和能力的考查。

2021年数学试题的变化

在6月21日下午所有科目都结束之后，终于看到了全卷及答案，如之前所料一般，与往年的试题相比，难度确确实有所降低，主要体现选择题最后一题、填空题最后一题、解答题最后两题上，基础中等偏上的学生基本上都能正确解答，估计今年中考数学会出现高分段扎堆的现象，110 的会比往年增加很多。

当然了，试题的难与易是相对的，即便题目难度不大，能考115 甚至是满分的还是少数，因为虽然压轴题的难度略有降低，但毕竟是压轴题，还是具有一定的区分度，其次，试卷结构的调整，解答题数量增加，对学生的做题速度有了更高的要求，对解题细节也有更高的要求，很多同学都会因为解题细节上的一些失误导致丢分，甚至会出现题目越简单月容易丢分。

在考完试跟学生和家长聊天的过程中，家长也提到，孩子试卷完成的不错，但在几处计算上丢分了，这十分可惜，估计在计算上丢分的学生不在少数，今年的试卷上涉及到直接考查计算的题目有所增加；还有部分学生凭借着模考最后一题的难度很大的经验，在最后一题只随便看了几眼，并没有进行过多的思考就给放弃了，怪可惜的，可以说，今年的最后一题是近些年来最简单的一题，只要细心思考，正确解答是没有多少问题的。

试卷满分120分，要求学生在120分钟内完成，本试卷包含选择题、填空题和解答题三种题型，今年的选择题题量由之前的10道降为8道，填空题由之前的4道增加到5道，解答题数量由之前的11道增加到13道，全卷的题量由之前的25道增加到26题。

虽然试卷结构发生了改变，但考查的重难点并没有多大的改变，填空题增加了一道以幻方为背景的题目，本质上是一道有理数的加减运算题，解答题中的计算题由之前的2道增加到3道，考查到实数的混合运算、解不等式组和解分式方程，这都是基础运算，解答题还增加了一道一元一次方程的应用题，这在近些年来是首例，但难度不大。

在今年中考之前网上就流传说，今年的中考试卷结构要调整，选择题数量减少，填空题和解答题数量增加，会增加某些考点，当时呼声最高的要属一元二次方程和新函数图像探究题，在最终中考中，试卷结构调调整，也出现了新考点，但并没有出现一元二次方程和新函数图像探究题。

在中考前对一元二次方程和新函数图像探究花费时间强化练习的也不要失望，虽然中考没有涉及到，但这两块内容在高中数学中有很多的应用，就算是为高中数学的学习提前打下基础吧。虽然今年没有考查到，但这两块内容走进中考也不是空穴来风，也许在之后的中考中会逐步加入，因此，希望目前初一、初二的学生在之后复习备考的时候不要忽视这两大考点。

考点1：有理数的乘法：

第1题考查有理数的乘法，直接应用有理数乘法法则进行运算即可；

考点2：轴对称图形的判断：

第2题考查轴对称图形的判断，根据定义判断即可，在之前几年考查视图的频率比较高；

考点3：负指数幂的运算：

第3题考查幂的运算，负指数幂的运算，负指数幂的底数是字母的情况在之没有出现过，但难度不大，直接利用负指数幂的运算法则进行运算即可。

考点4：三角形的内角定理：

第4题考查角度的计算，在之前的中考中考查应用平行线的性质计算角度的频率较高，这道题考查应用三角形的内外角定理计算角度。

考点5：菱形的性质：

第5题考查菱形的性质，含有60度角菱形比较特殊，根据菱形的性质进行计算即可，也可直接利用考前强调的一组数据，含有120度的等腰三角形的三边比为1:1：根号3直接计算即可。

考点6：一次函数的图像与性质：

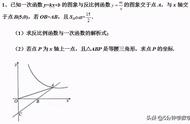
第6题考查一次函数图像的平移，根据图像平移的规律“左加右减”代入计算即可，因为k为2，所以需要添加括号，这一步比较 容易出错，表示出平移后的直线后，再根据平移后是正比例函数，即过原点，得到关于字母m 的方程，解方程即可。

考点7：等腰三角形和全等三角形：

第7题考查等腰三角形及全等三角形，属于到目前为止难度略微提升的题目，需要做辅助线，但很容易想到，就是过顶点向底边做垂线，做完垂线后出现一堆k字全等三角形，利用全等三角形和等腰三角形的性质进行计算即可，涉及到最基本的全等k字模型。

考点8：二次函数的图像与性质

第8题考查的是二次函数的图像与性质，已经给出四组数据，可以用待定系数法求出函数关系式，然后再逐个分析即可；对于这道题目，还可以直接描点、画出草图，根据图像直接进行分析和判断即可，画图时需要注意几个特殊点和线，与y轴交点、顶点、对称轴等。虽然一般选择题的最后一题是选择题的压轴题，但这道题目比较常规，应该属于近几年来选择题压轴题二次函数的图像与性质中最简单的一题。

整体来看，选择题这8题都没有难度，属于常规考点和考法，但要注意解题思路，像第6题需要注意直线平移的特征，第7题需要做辅助线，第8题需要画草图分析，基础扎实的学生完全可以在五分钟之内完成，但切记，保证准确率是前提。

考点9：因式分解

第9题考查因式分解，在进行中考中，很少直接考查因式分解，一般都是在分式的运算中考查，但在模考中经常出现，本题考查到提公因式法和公式法分解因式，比较基础。

考点10：正多边形的性质

第10题考查正多边形的内外角和定理，近年来一般都是结合三角形进行考查，但今年直接考查，难度更低了，直接利用外角和等于360度，算出一个外角的度数，再利用内外角互补即可计算出内角的度数。

考点11：幻方

第11题以幻方为背景，抓住特征：各行、各列、各对角线上的数字之和相等，直接计算即可，本质上是有理数的加法运算，但题目立意较新，理清题意是解题的关键。

考点12：反比例函数的图像与性质

第12题考查到反比例函数的图像与性质，根据m的取值范围确定反比例函数的k值，作出草图，根据性质直接进行分析和判断即可，这道题考查的比较直接和基础，没有难度。

考点13：几何动点最值

第13题是一道几何动点最值问题，以正方形和圆为背景，求正方形的顶点A到圆上一点的最大距离，解题的关键是确定最大值时圆的位置，虽然是一道动圆问题，但比较简单，即便不会分析，也能想到当圆在顶点C附近时，距离最大，也就是当圆与CB和CD都相切时，圆心o在对角线AC上时，能取得最大值，再利用圆外一点到圆上一点的最大距离等于圆外一点到圆心的距离再加上半径，进行计算即可。

整体来看，填空题的4题都是比较简单的，都属于一眼可以看出思路甚至是看出答案的题目，第13题因为涉及到动点，难度略大，算得上是到目前为止，难度较大的一题，估计很多学生做到这题时才明白平时练了那么多的几何综合动点题终于没白费。

考点14：实数的混合运算

第14题是实数的综合运算题，涉及到零指数幂、去绝对值和二次根式化简运算，相信这样的题在平时练习的太多了，在去绝对值的这一步容易出错。

考点15：解不等式组

第15题考查解不等式组，去年中考也考到了解不等式组，在今年模考中解不等式组肯定被大量练习了，应该没有问题，注意符号即可。

考点16：解分式方程

第16题考查解分式方程，需要注意当分母能因式分解的时，需要先进行因式分解，然后找最简公分母，再约分，化为整式方程，需要注意要验根哦。

练习考查三道基本运算，应该属于送分题，但从目前了解的情况来看，很多学生似乎并没有将这些分数完全收入囊中，有些可惜了。