虽然2020美国大选现在还未出正式结果,但其跌宕起伏的剧情,注定会写入历史,成为长盛难衰的争议话题。目前,在推特等社交媒体上,就开始涌现一种说法,认为经分析统计各候选人在某地所有选区的得票数,发现特朗普一切正常,而拜登的得票情况不符合“本福特定律”,涉嫌舞弊。

在国内,“拜登得票数偏离‘本福特定律’”的话题也冲上了网络热搜榜。

需要明确的是,社交媒体的上述说法缺少法律和相关专业背书,听听就好,不过牵扯出的“本福特定律”确实大有来头,它已经在会计信息、统计资料、税收和金融等领域发光发热,做统计和审计的小伙伴应该都听说过它。
让人情有独钟的数字1935年,美国通用电气公司的科学家弗兰克.本福特在图书馆翻阅数学对数表时,偶然发现头几页被更多的人翻阅,显得比后面的更脏一些,这一现象引起了他的极大兴趣。
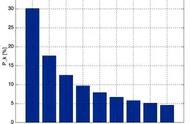
本福特经过进一步的研究发现,只要统计的样本数量足够多,同时数据又没有特定的上限和下限,那么数据中以1开头的数字出现的频率是最高的,达到30%,以2开头的数字出现频率为17.6%,以3开头的数字为12.5%,也就是说,随着数字的增大,出现的频率依次减少,具体见下图。

本福特将这一规律推导成一个公式F(d)=lg[1 1/d],公式中F代表使用频率,d代表待求证数据的第一个数字。这就是著名的“本福特定律”,又叫“第一数字定律”。
后来,本福特对其它类型的数据进行了研究,包括人口、死亡率、物理和化学常数、半衰期放射性同位素、物理课本中的答案、素数数字以及斐波那契数列,发现都有这一定律的身影。简单说,只要是由度量单位制获得的数据,都符合“本福特定律”。
造假账者胆战心惊“本福特定律”面世后,应用最广的领域是统计、审计领域,因为造假账者总是试图在账目中隐藏数据,结果使假账中的数字分布不符合“本福特定律”,从而露出马脚。
2001年,美国最大的能源交易商、全球500强企业排行榜名列第7的安然公司突然宣布*,接着传出该公司涉嫌做假账的丑闻。事后,有人发现,安然公司在2001年度到2002年度公布的每股盈利数字完全不符合“本福特定律”,说明安然公司的管理层确实改动过数据。