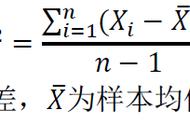任意选取两个这样的数进行加减乘除运算，其结果也永远是上面这种形式的数。由此可知，所有具有这种形式的数构成了域。

以上举出的域只不过是无数个域中的两三个实例，这些域中都包含着无穷多个数。不过，并不是所有域中都一定包含无穷多个数，也存在一些由有限多个数构成的域。

由有限多个数构成的域叫作「有限域」。由于最初研究有限域的数学家为伽罗瓦，所以我们也将有限域称为“伽罗瓦域”。

在有限域中，数的个数最少为 2。

这个域就是用 (mod 2) 对整数进行分类时的剩余类。

用 (mod 2) 进行分类后，整数将被分为两类，一是包含 0 的类，即偶数；二是包含 1 的类，即奇数。我们在此假设，所有偶数用 0 表示，所有奇数用 1 表示。

大家可能觉得 1 1 = 0 有些奇怪，但只要把它看作是奇 奇 = 偶的意思就很好理解了，或者也可以认为它的意思等同于 1 1 ≡ 0 (mod 2)。

乘法运算的情况如下。

具有上述 和 × 的计算规则的 0 和 1 的集合就构成了域。

根据"同余式与等式"一节介绍可知，利用 (mod n) 对整数分类后，- 和 × 等各种运算规则仍然成立。

当然，对于 (mod 2) 应该也成立。

另外，对于非 0 的“数”，也就是 1 而言，其逆元*为 1 本身，所以 ÷1 和 ×1 的结果相同。

* 通常在数学领域它与“倒数”的意思相同，指该“数”乘以“某数”等于 1 时的“某数”。

也就是说，{0, 1} 这个“数”的集合构成了域。

下面我们来看看 (mod 3) 的情况。

剩余类包含 0，1，2 这三类。加法运算和乘法运算如下表所示。