(2)
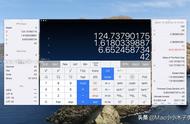
Det(A)表示矩阵A的行列式,П表示连乘,sgn表示符号,在某些情况下是正的,另外一些情况下是负的。Sn表示n个元素的置换群,也就是将1、2、3…n这些元素进行全排列。公式大体意思是:将一些元素ai,σ(i)连乘,更换顺序后再连乘...然后再把它们做加法或者减法,就可以得到行列式。
行列式有很大的用处,而且,行列式有很多很好的性质,使得它可以找到更好的算法,降低计算复杂度。根据数学家们的计算,n阶行列式计算复杂度为O((log2)^n)级别,也就是:

计算1万亿阶的矩阵的行列式,计算复杂度也在100多步骤。行列式真是个物美价廉的好东西。
3 积和式不过,行列式的亲兄弟——积和式就不这么友善了。它和行列式长得很像,只是行列式有加也有减,积和式全都是加。
例如:二阶积和式

N阶积和式

(3)
对比行列式的表达式(2),我们会发现它们都是对角标轮换后相乘再相加。只不过行列式有一个符号函数,有时取正有时取负,而积和式把所有的负号都去掉,变成了完全相加。
尽管只有这么一点点差别,但是积和式却没有行列式那么好的性质,计算复杂度非常高。按照目前最优的算法,n阶积和式的计算复杂度是O(nx2n), 随着n的增大,复杂度指数级上升。