17解:反比例函数的图像与性质.

因点A在y=3/x上,故设A(m,3/m),因AB∥x轴,且点B在y=12/x上,故B(4m,3/m),因AC=BC,故点C在AB的垂直平分线上,又点C在y=12/x上,故C(5m/2,24/ 5m),所以△ABC的面积等于

½(4m-m)(24/5m -3/m)=27/10.

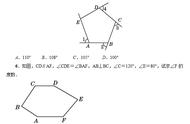
18解:扇形的面积公式,球阴影部分的面积.

扇形ADE的面积等于扇形ABC的面积,等于πr²/4=9π.连接BD,则BA=BD=

AD=6,△ABD是等边三角形,扇形ABD的面积等于πr²/6=6π,△ABD的面积等于√3r²/4=9√3,所以阴影部分的面积等于9π-(6π-9√3)=3π 9√3.

19解:分式的化简与运算,一元一次不等式组的解法.

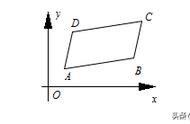
20解:平行四边形的性质,三角函数值的求解.

(1)在Rt△AED中,AE=ADCosA

=8,故DE=15,所以平行四边形ABCD的面积等于DE×AB=15×20=300.(2)BE=AB-AE=12,故△BCE的面积等于½DE×BE=90.在RT△CDE中,CE=25,作BF⊥CE于F,故△BCE的面积等于½BF×CE=25/2 BF,故BF=36/5,故在Rt△BFC中,

sin∠BCE=BF/BC=36/85.

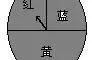
21解:概率.

(1)若小晗任意按下一个开关,正好楼梯灯亮的概率是1/3.

(2)画树状图或列表略.任意按下其中两个开关,等可能的结果有AB,AC,BA,BC,CA,CB共6种,正好是客厅灯和走廊灯同时亮的结果有2种,故所求概率为2/6=1/3.