人教版六年级数学上册
易错题集锦
一、填空题。
1、一种盐水的含盐率是20%,盐与水的比是( )。
2、生产同样多的零件,小张用了4小时,小李用了6小时,小张和小李工作效率的最简比是( )。
3、从甲地到乙地,客车要行驶4时,货车要行驶5时,客车的速度与货车的速度比是( ),货车的速度比客车慢( )%。
4、100克糖溶在水里,制成的糖水的含糖率为12.5%,如果再加200克水,这时糖与糖水的比是( )。
5、若从六(1)班调全班人数的1/10到六(2)班,则两班人数相等,原来六(1)班与六(2)班的人数比是( )。
6、把甲队人数的1/4调入乙队,这时两队人数相等,甲队与乙队原人数的比为( )。
7、六(1)班今天到校40人,请病假的5人,该班的出勤率是( )。
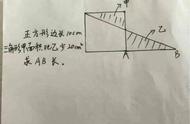
8、把一个半径是10cm的圆拼成接成一个近似的长方形后,长方形的周长是( ),面积是( )。
9、( )米比9米多40% , 9米比( )少55% ,200千克比160千克多( )%;160千克比200千克少( )%;16米比( )米多它的60%;( )比32少30% 。
10、钟面上时针的长1dm,一昼夜时针扫过的面积是( )。
11、一根水管,第一次截去全长的1/4,第二次截去余下的2/3,两次共截去全长的( )。
12、某种皮衣价格为1650元,打八折出售可盈利10%.那么若以1650元出售,可盈利( )元。
13、正方形边长增加10%,它的面积增加( )% 。
二、判断题。
1、某商品先提价5%,后又降阶5%,这件商品的现价与原价相等。( )
2、在含盐20%的盐水中加入同样多的盐和水后,盐水的含盐率不变。( )
3、如果甲数比乙数多25%,那么乙数就比甲数少25%。 ( )
4、半径是2厘米的圆,它的周长和面积相等。 ( )
5、直径相等的两个圆,面积不一定相等。 ( )
6、比的前项和后项都乘或除以同一个数,比值大小不变。 ( )
三、选择题。
1、数学小组共有20名学生,则男、女人数的比不可能是( )。
A.5︰1 B.4︰1 C.3︰1 D.1︰1
2、如图,阴影部分的面积相当于甲圆面积的1/6,相当于乙圆面积的1/5,那么乙与甲两个圆的面积比是( )。

A、6︰1 B、5︰1 C、5︰6 D、6︰5
3、一杯牛奶,牛奶与水的比是1︰4,喝掉一半后,牛奶与水的比是( )。
A、1︰4 B、1︰2 C、1︰8 D、 无法确定
4、利息与本金相比( )
A、利息大于本金 B、利息小于本金 C、利息不一定小于本金
四、解决问题。
1、A、B两地相距408KM,客车和货车同时从A、B两地相对开出,3小时后相遇,已知客车和货车的速度比是9:8,客车每时比货车每时快多少千米?
2、东岗小学组织学生收集树种,五年级收集的树种占总质量的40%,六年级收集的树种占质量的50%,五年级收集的树种比六年级少20千克。五六年级一共收集树种多少千克?
3、一件商品按20%的利润定价,然后又按8折出售,结果亏了64元,这件商品的成本是多少元?
4、将一根384cm的铁丝焊成一个长、宽、高的比是3:2:1的长方体模型。这个模型的长、宽、高各是多少厘米?表面积是多少平方厘米?
5、一块长方形土地,周长是160m,长和宽的比是5:3,这块长方形土地的面积是多少平方米?
6、李明和张华参加赛跑,李明跑到中点时,张华跑了全程的40%,此时两人相距80米,你知道赛程多少米吗?
*7、看一本书,第一天读的页数与未读页数的比是1:3,第二天看了120页,这时已读的与未读页数的比是2:3,这本书有多少页?
参考答案
一、填空题。
1、一种盐水的含盐率是20%,盐与水的比是(1:4)。
2、生产同样多的零件,小张用了4小时,小李用了6小时,小张和小李工作效率的最简比是(3:2)。
【解析:将这批零件看作单位“1”,则小张的工作效率为:1÷4=1/4 小李的工作效率为:1÷6=1/6 两人的工作效率比为:1/4:1/6,化简后就是3:2】
3、从甲地到乙地,客车要行驶4时,货车要行驶5时,客车的速度与货车的速度比是(5:4),货车的速度比客车慢(20)%。
【解析:求速度比的方法同第2题。货车的速度比客车慢((5-4)÷5=20%)】
4、100克糖溶在水里,制成的糖水的含糖率为12.5%,如果再加200克水,这时糖与糖水的比是(1:10)。
【解析:此题关键是要先算出原来的糖水是多少克:100÷12.5%=800(克)。再求加水后糖与糖水的比:100:(800 200)=100:1000=1:10】
5、若从六(1)班调全班人数的1/10到六(2)班,则两班人数相等,原来六(1)班与六(2)班的人数比是(5:4)。
【解析:用方程来解答:设六(1)人数有a人,六(2)班人数有b人。根据题意列出方程后并求解:

通过解方程得出a与b的比为10:8,即六(1)班与六(2)班的人数为10:8,化简后为5:4。 】
6、把甲队人数的1/4调入乙队,这时两队人数相等,甲队与乙队原人数的比为(2:1)。
【解析:方法同第5题。】
7、六(1)班今天到校40人,请病假的5人,该班的出勤率是(88.9%)。
【解析:用到校人数就是出勤人数。出勤人数÷全班人数×100%=出勤率。40÷(40 5)×100%≈88.9%】
8、把一个半径是10cm的圆拼成一个近似的长方形后,长方形的周长是(82.8cm),面积是(314cm2)。
【解析:拼成的长方形的周长就是这个半径为10cm的圆的周长与两个半径的和:3.14×10×2 10×2=82.8cm;长方形的面积等于圆的面积,那么面积就是:3.14×10×10=314平方厘米。】
9、(12.6)米比9米多40%【9×(1 40%)=12.6】 , 9米比(20)少55%【9÷(1-55%)=20】 ,200千克比160千克多(25)%【(200-160)÷160=25%】;160千克比200千克少(20)%【(200-160)÷200=20%】;16米比(6.4)米多它的60%【16×(1-60%)=6.4 注意:“它”是指16。】;( 22.4 )比32少30%【32×(1-30%)=22.4】 。
【解析:本题主要是考查 单位“1”(总量)、对应量、对应分率之间的关系。单位“1”(总量)×对应分率=对应量】
10、钟面上时针的长1dm,一昼夜时针扫过的面积是(2π dm2)。
【解析:时针的长就是圆的半径,“一昼夜”指24小时,时针走了24小时就是走了两周。π×1²×2=2π(dm²)】
11、一根水管,第一次截去全长的1/4,第二次截去余下的2/3,两次共截去全长的(3/4)。
【解析:1/4 (1-1/4)×2/3=3/4】
12、某种皮衣价格为1650元,打八折出售可盈利10%。那么若以1650元出售,可盈利(450)元。
【解析:本题关键是要先算出进价,原题中的“10%”是针对进价的。设皮衣的进价为x元。(1 10%)x=1650*80% 解得:x=1200。以1650元出售,可盈利:1650-1200=450(元)】
13、正方形边长增加10%,它的面积增加(21)% 。
【解析:{[1×(1 10%)]2-1}÷1=21%】
二、判断题。
1、某商品先提价5%,后又降阶5%,这件商品的现价与原价相等。(×)
【解析:错。两个5%的单位“1”不一样。1×(1 5%)×(1-5%)=0.9975 值小于1表示现价比原价少,值大于1表示多。】
2、在含盐20%的盐水中加入同样多的盐和水后,盐水的含盐率不变。(×)
【解析:错。用假设法来验证:假设盐是20克,水是80克,则含盐就是20%。如果分别同时加入10克盐和水,那么这时含盐率就是:(20 10)÷(20 10 80 10)×100%=25%,含盐率变大了。】
3、如果甲数比乙数多25%,那么乙数就比甲数少25%。 (×)
【解析:错。两个25%相对的单位1不同。应该是:甲数比乙数多25%,乙数就比甲数少20%。25%÷(1 25%)=20%】
4、半径是2厘米的圆,它的周长和面积相等。(×)
【解析:错。只能说在数值上相等,但是万物都有单位,周长单位是1维的,面积单位是2维的,怎么可能相等呢?简单地说,周长和面积单位不一样,也不可能互化,所以周长和面积不可能相等。】
5、直径相等的两个圆,面积不一定相等。(×)
【解析:错,是一定相等。直径相等就表示半径也会相等,而半径决定了圆的大小,只要圆的半径相等,它们的大小就会相等,即面积也一定相等。】
6、比的前项和后项都乘或除以同一个数,比值大小不变。(×)
【解析:错。0必须除外。0是不能作为除数的。】
三、选择题。
1、数学小组共有20名学生,则男、女人数的比不可能是(A)。
A.5︰1 B.4︰1 C.3︰1 D.1︰1
【解析:A。20的因数有:1、2、4、5、10、20,而5 1=6,6不是20的因数;所以不可能是5:1。】
2、如图,阴影部分的面积相当于甲圆面积的1/6,相当于乙圆面积的1/5,那么乙与甲两个圆的面积比是(C)。

A、6︰1 B、5︰1 C、5︰6 D、6︰5
3、一杯牛奶,牛奶与水的比是1︰4,喝掉一半后,牛奶与水的比是(A)。
A、1︰4 B、1︰2 C、1︰8 D、 无法确定
【解析:A。喝掉一半后,浓度不变,牛奶与水的比还是1:4。验证:(1-1×1/2):(4-4×1/2)=1:4】
4、利息与本金相比(C)
A、利息大于本金 B、利息小于本金 C、利息不一定小于本金
【解析:C。利率表示利息与本金的比率;利息可能小于本金,也可能大于本金;所以利息不一定小于本金。】
四、解决问题。
1、A、B两地相距408km,客车和货车同时从A、B两地相对开出,3小时后相遇,已知客车和货车的速度比是9:8,客车每时比货车每时快多少千米?
解:设客车速度为9x,货车速度为8x,根据题意列方程:
(9x 8x)×3=408
17x*3=408
x=408/51
x=8
所以客车每小时比货车快:9x-8x=x=8(千米)
2、东岗小学组织学生收集树种,五年级收集的树种占总质量的40%,六年级收集的树种占总质量的50%,五年级收集的树种比六年级少20千克。五六年级一共收集树种多少千克?
20÷(50%-40%)=200(千克)
3、一件商品按20%的利润定价,然后又按8折出售,结果亏了64元,这件商品的成本是多少元?
解:设这件商品的成本是 x 元
x - 64=[(1 20%)x] ×80%
x - 64=1.2x × 0.8
x - 64=0.96x
x-0.96x=64
0.04x = 64
x = 64÷0.04
x = 1600
答:这件商品的成本是1600 元。
【说明:8折表示按定价的80%出售。x - 64表示现价,(1 20%)x表示定价,[(1 20%)x] ×80% 表示打8折后的售价,即现价。】
4、将一根384cm的铁丝焊成一个长、宽、高的比是3:2:1的长方体模型。这个模型的长、宽、高各是多少厘米?表面积是多少平方厘米?
先算出一条长、一条宽、一条高的和:
384÷4=96cm;
再计算长宽高各是多少:
长:96÷(3 2 1)×3=48cm
宽:96÷(3 2 1)×2=32cm
高:96÷(3 2 1)×1=16cm;
表面积:
(48×32 48×16 32×16)×2=5632(cm2)
5、一块长方形土地,周长是160m,长和宽的比是5:3,这块长方形土地的面积是多少平方米?
长:160÷2÷(5 3)×5=50m
宽:160÷2÷(5 3)×3=30m
面积:50×30=1500(m2)
6、李明和张华参加赛跑,李明跑到中点时,张华跑了全程的40%,此时两人相距80米,你知道赛程多少米吗?
分析:把整个赛程看作单位“1”,那么80米对应的分率是(50%-40%),根据分数除法的意义,用对应量除以对应的分率即可.
解答:
80÷(50%-40%)
=80÷10%
=800(米)
答:这个赛程长800米。
点评:解答此题的关键是找单位“1”,然后用对应量除以对应的分率解决问题。
*7、看一本书,第一天读的页数与未读页数的比是1:3,第二天看了120页,这时已读的与未读页数的比是2:3,这本书有多少页?

打印方法:发送本文至电脑端,打开链接后按ctrl P调出打印机,显示完整预览后即可打印。